Given :-
- Slope of the line is -3/2 .
- It passes through (-3,3) .
To Find :-
- The equation of the line .
Solution :-
Here it's given that ,
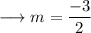
And a point that is (-3,3) . We can use the point slope form of the line which is ,
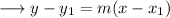
Substituting the respective values,
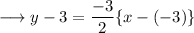
Simplify,
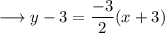
Simplify by opening the brackets ,
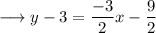
Add 3 on both sides ,
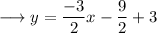
Add ,
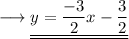
This is the required answer in slope intercept form .