Question

Graph 2x + y > 6Test point :

Answer 1

We have to graph the inequality:

`2x+y>6`

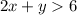
We have to write the line that represent the boundary between the solution region and the other region.

We can write the equation of this line as:

`\begin{gathered} 2x+y=6 \\ y=-2x+6 \end{gathered}`

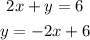
This line has the y-intercept at (0,6).

We can find another point of this line by giving a value to x, for example x = 3:

`y(3)=-2(3)+6=-6+6=0`

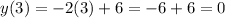
Then, the point (3, 0) also belongs to this line.

We can graph the line that limit this two regions as:

Now, if we look at the inequality, this line does not belong to the solution region as we have a ">" sign.

We can find which of the two regions is the solution region by testing one point.

For example, we can test for (0,0):

`\begin{gathered} 2(0)+0>6 \\ 0>6\longrightarrow\text{False} \end{gathered}`

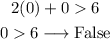
Then, (0,0) is outside of the solution region. Then, the solution region is above the line y = -2x + 6: