Question

Find the pattern in each sequence and use it to list the next two terms. a. 5, 17, 29, 41, b. 18, 14, 10, 6, c. -9,4,-8,5, -7,6,

Answer 1

Given:

The objective is to find the pattern and list out the next two terms in the sequence.

Step-by-step explanation:

a)

The given sequence is 5, 17, 29, 41....

Let's find the difference between the two successive terms of the sequence.

`\begin{gathered} d=17-5=12 \\ d=29-17=12 \\ d=41-29=12 \end{gathered}`

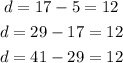
Thus, the common difference between each successive terms is 12.

Then, the next two terms can be calculated as,

`\begin{gathered} 41+12=53 \\ 53+12=65 \end{gathered}`

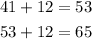
Hence, the next two terms are 53 and 65.

b)

The given sequence is 18, 14, 10, 6...

Let's find the difference between the two successive terms of the sequence,

`\begin{gathered} d=14-18=-4 \\ d=10-14=-4 \\ d=6-10=-4 \end{gathered}`

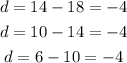
Thus, the common difference between each successive terms is -4.

Then, the next two terms can be calculated as,

`\begin{gathered} 6-4=2 \\ 2-4=-2 \end{gathered}`

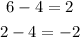
Hence, the next two terms are 2 and -2.

c)

The given sequence is -9, 4, -8, 5, -7, 6.

Here it can be observed that starting from -9, the alternate numbers are increasing.

Then, the next number can be calculated by find the difference between those sequence provided with alternae places.

`\begin{gathered} d=-8-(-9)=1 \\ d=-7-(-8)=1 \end{gathered}`

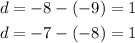
Thus, the common difference between each successive terms is 1.

Similarly, the commo difference between the series present inside is,

`\begin{gathered} d=5-4=1 \\ d=6-5=1 \end{gathered}`

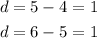
Then, the next two number will be,

`\begin{gathered} -7+1=-6 \\ 6+1=7 \end{gathered}`

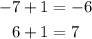
Hence, the two numbers are -9, 4, -8, 5, -7, 6, -6, 7.