Question

All you need is on the photo this is a homework

Answer 1

We have the quadratic function:

`f(x)=x^2-4x-12`

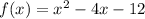
1) We have to factorize it in this way:

`f(x)=(x-x_1)(x-x_2)`

To do that we have to find the roots x1 and x2.

We can apply the quadratic formula as:

`\begin{gathered} f(x)=ax^2+bx+c\longrightarrow x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(-4)\pm\sqrt[]{(-4)^2-4\cdot1\cdot(-12)}}{2\cdot1} \\ x=(4)/(2)\pm\frac{\sqrt[]{16+48}}{2} \\ x=2\pm\frac{\sqrt[]{64}}{2} \\ x=2\pm(8)/(2) \\ x=2\pm4 \\ x_1=2-4=-2 \\ x_2=2+4=6 \end{gathered}`

We have the values of both of the roots, so we can factorize f(x) as:

`f(x)=(x+2)(x-6)`

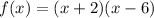
2) We have to express f(x) in vertex form.

To do that we can rearrange the expression as:

`\begin{gathered} x^2-4x-12 \\ x^2-4x+4-4-12 \\ (x^2-4x+4)-16 \\ (x-2)^2-16 \end{gathered}`

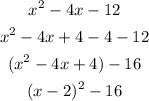
The vertex form for f(x) is:

`f(x)=(x-2)^2-16`

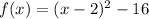
3)

a) The x-intercepts are the roots of the function: x1=-2 and x2=6. For this values of x, the function has a value of 0. X-intercepts can be expressed as (-2,0) and (6,0).

b) The y-intercept is given by the independent value in the equation, c=-12. The is the value of the function when x=0, that is, f(0)=-12. It can be expressed as (0,-12).

c) The vertex is (2,-16) and can be deduced from the vertex expression f(x)=(x-2)^2-16.

d) The axis of symmetry, as it is a parabola, is a vertical axis that pass through the vertex. Then, its definition is x=2, as the vertex is at (2,-16).

e) The quadratic funtion in this case, as the quadratic coefficient is positive, has a minimum.

f) The minimum is located at the vertex and has a value of y=-16.