Question

Suppose that the function g is defined, for all real numbers, as follows. x < - 1; g(x)= 2&ifx<-1\\ 3&ifx=-1\\ -1&ifx>-1; x = - 1; x > - 1 Graph the function g.

Answer 1

The given piecewise-defined function is:

`g(x)=\begin{cases}{2\qquad\text{ if }x<-1} \\ {3\qquad\text{ if }x=-1} \\ {-1\qquad\text{ if }x>-1}\end{cases}`

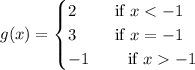
It is required to graph the function.

To do this, graph each piece with respect to the corresponding domain.

Graph g(x)=2 over x<-1:

Notice that an open circle is at x=-1 since it is not included in the interval x<-1.

Graph g(x)=3 for x=-1. This is just a point:

Finally, graph g(x)=-1 for x>-1:

There is an open circle at x=-1 since it is not included in the interval x>-1.

Thus, the required graph of the piecewise-defined function is shown below: