Given
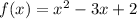
Find
Rewrite it into standard form and identify vertex and all its intercepts.
Step-by-step explanation
standard form =
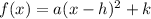
where (h , k) be the vertex
so ,
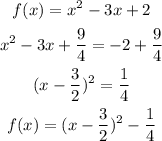
so vertex be
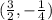
for intercept put f(x) = 0
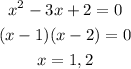
so , x - intercept = (1 , 0) and (2 , 0)
for y- intercept put x =0
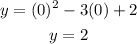
y - intercept (0 , 2)
Final Answer
Therefore , vertex is (3/2,-1/4)
x - intercept = (1 , 0) and (2 , 0) and y - intercept (0 , 2)