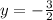Question

How to find the vertex calculus 2What is the vertex, focus and directrix of x^2 = 6y

Answer 1

Given:

`x^2=6y`

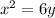
Part A:

The vertex of an up-down facing parabola of the form;

`\begin{gathered} y=ax^2+bx+c \\ is \\ x_v=-(b)/(2a) \end{gathered}`

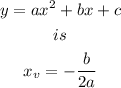
Rewriting the equation given;

`\begin{gathered} 6y=x^2 \\ y=(1)/(6)x^2 \\ \\ \text{Hence,} \\ a=(1)/(6) \\ b=0 \\ c=0 \\ \\ \text{Hence,} \\ x_v=-(b)/(2a) \\ x_v=-(0)/(2((1)/(6))) \\ x_v=0 \\ \\ _{} \\ \text{Substituting the value of x into y,} \\ y=(1)/(6)x^2 \\ y_v=(1)/(6)(0^2) \\ y_v=0 \\ \\ \text{Hence, the vertex is;} \\ (x_v,y_v)=(h,k)=(0,0) \end{gathered}`

Therefore, the vertex is (0,0)

Part B:

A parabola is the locus of points such that the distance to a point (the focus) equals the distance to a line (directrix)

Using the standard equation of a parabola;

`\begin{gathered} 4p(y-k)=(x-h)^2 \\ \\ \text{Where;} \\ (h,k)\text{ is the vertex} \\ |p|\text{ is the focal length} \end{gathered}`

Rewriting the equation in standard form,

`\begin{gathered} x^2=6y \\ 6y=x^2 \\ 4((3)/(2))(y-k)=(x-h)^2 \\ \text{putting (h,k)=(0,0)} \\ 4((3)/(2))(y-0)=(x-0)^2 \\ Comparing\text{to the standard form;} \\ p=(3)/(2) \end{gathered}`

Since the parabola is symmetric around the y-axis, the focus is a distance p from the center (0,0)

Hence,

`\begin{gathered} Focus\text{ is;} \\ (0,0+p) \\ =(0,0+(3)/(2)) \\ =(0,(3)/(2)) \end{gathered}`

Therefore, the focus is;

`(0,(3)/(2))`

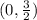
Part C:

A parabola is the locus of points such that the distance to a point (the focus) equals the distance to a line (directrix)

Using the standard equation of a parabola;

`\begin{gathered} 4p(y-k)=(x-h)^2 \\ \\ \text{Where;} \\ (h,k)\text{ is the vertex} \\ |p|\text{ is the focal length} \end{gathered}`

Rewriting the equation in standard form,

`\begin{gathered} x^2=6y \\ 6y=x^2 \\ 4((3)/(2))(y-k)=(x-h)^2 \\ \text{putting (h,k)=(0,0)} \\ 4((3)/(2))(y-0)=(x-0)^2 \\ Comparing\text{to the standard form;} \\ p=(3)/(2) \end{gathered}`

Since the parabola is symmetric around the y-axis, the directrix is a line parallel to the x-axis at a distance p from the center (0,0).

Hence,

`\begin{gathered} Directrix\text{ is;} \\ y=0-p \\ y=0-(3)/(2) \\ y=-(3)/(2) \end{gathered}`

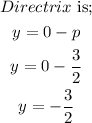
Therefore, the directrix is;

`y=-(3)/(2)`