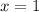Question

Find the axis of symmetry and vertex for the parabola y=−5x^2+10x−6.

Answer 1

Revision

- General equation of a parabola:

`y=a\cdot(x-h)^2+k`

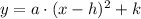
- Coordinates of the vertex of a parabola:

`(h,k)`

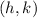
- Axis of symmetry of the parabola:

`x=h`

Answer

We have the following parabola:

`y=-5x^2+10x-6`

We can read the coordinates of the vertex and axis of symmetry from the equation of a parabola if we express its equation in the general form above. To do that we will "complete squares" in the following way:

`\begin{gathered} y=-5(x^2-2x)-6 \\ y=-5(x^2-2x+1-1)-6 \\ y=-5(x^2-2x+1)+5-6 \\ y=-5(x-1)^2-1 \end{gathered}`

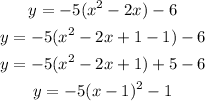
Comparing this equation with the general equation of the parabola, we see that:

`\begin{gathered} h=1 \\ k=-1 \end{gathered}`

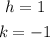
So the coordinates of the vertex are:

`(1,-1)`

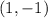
and the axis symmetry is:

`x=1`