We have to find sin(2x), cos(2x) and tan(2x).
We know that sin(x) = 1/√10 and x belongs to the first quadrant.
The last means that 2x belongs to the first or the second quadrant.
sin(2x) will then be positive but cos(2x) can be either positive or negative, depending on the quadrant.
We can use the following identiy for sin(2x):
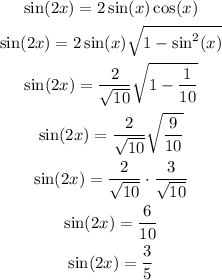
We can now calculate cos(2x) as:
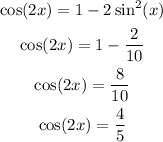
Finally, we can calculate tan(2x) as:
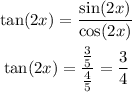
Answer:
sin(2x) = 3/5
cos(2x) = 4/5
tan(2x) = 3/4