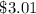Question

In January, Joanna deposited $250into her savings account. InFebruary, she deposited anadditional $100. If her account hasan APR of 6% compounded monthly,how much interest did Joanna earnin the first two months?

Answer 1

Given:

In January Joanna deposited $250 into her savings account.

In February, she deposited an additional $100.

Her account has an APR of 6% compounded monthly.

Required:

We have to find how much interest did Joanna earn in the first two months.

Step-by-step explanation:

For the month of January:

`A=P(1+(r)/(100))^n`

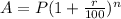
Here, P=$250, r=6%, amd n= 1 month=1/12 year.

Then,

`\begin{gathered} A=250(1+(6)/(100))^{(1)/(12)} \\ \\ A=250((106)/(100))^{(1)/(12)} \end{gathered}`
`\begin{gathered} A=250*1.005 \\ A=\text{ \$}251.25 \end{gathered}`

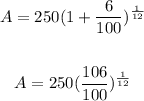
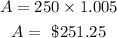
Then the interest is

`I=A-P=251.25-250=\text{ \$}1.25`

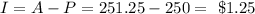
For the month of February:

P=251.24+100=351.25

Then we have

`\begin{gathered} A=351.25(1+(6)/(100))^{(1)/(12)} \\ \\ A=351.25((106)/(100))^{(1)/(12)} \end{gathered}`
`\begin{gathered} A=351.5*1.005 \\ A=\text{ \$}353.01 \end{gathered}`

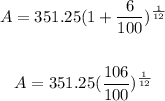
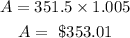
Then the interest is

`A=P-I=353.01-351.25=\text{ \$}1.76`

Therefore, the total interest is

`1.25+1.76=\text{ \$}3.01`

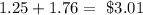
Final answer:

Hence the final answer is

`\text{ \$}3.01`