Question

i’m not sure how to do this please help me find the vertex, axis of symmetry, point at x axis, point at y intercept, and whether it has a minimum or maximum

Answer 1

Given:

`y=x^2+2x-24`

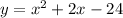
First, we will rewrite this equation by performing completing the square in order to get to the parabola's vertex form:

`y=a(x-h)^2+k`

Now, from the general form of the equation, let us perform completing the square.

`y=x^2+2x-24\rightarrow y=(x^2+2x+\_)-24-\__{}`

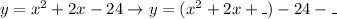
*Divide the coeffient of x by 2, and then square it

`y=(x^2+2x+((2)/(2))^2)-24-((2)/(2))^2`
`y=(x^2+2x+1)-24-1^{}`

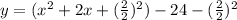
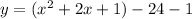
*Simplify

`y=\mleft(x+1\mright)^2-25`

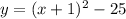
Now that we got the vertex form of the equation of the parabola, we can now solve for what is being asked.

First, the vertex of the parabola lies on (h, k)

Given that the equation of the parabola goes as:

`y=a(x-h)^2+k`

And we have

`y=(x+1)^2-25`

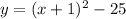
This would mean that:

h = -1

k = -25

Therefore, the vertex is at ( -1, -25)

Next, the axis of symmetry is noted as

`x=h`

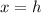
From the equation, we have

`(x+1)\rightarrow x=-1`

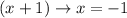
Therefore, the axis of symmetry is at x = -1.

Next, to find the points at the x-intercepts, using this equation, we will use y=0, and then solve of x.

`0=(x+1)^2-25`
`0=x^2+2x^{}-24`

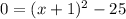
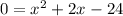
*Factor

`0=(x+6)(x-4)`
`x+6=0|x-4=0`

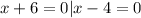
*Solve individually for x

`x+6=0`
`x=-6`
`x-4=0`

`x=4`

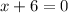
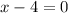
Therefore, the points at x-intercepts are (-6, 0) and (4,0)

To find the point at y-intercept, we will equate x = 0.

`y=(0+1)^2-25`
`y=(1)^2-25`
`y=1-25`
`y=-24`

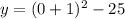
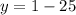
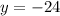
Therefore, the point at y-intercept is at ( 0, -24)

Lastly, to know if it has a maximum or a minimum, we'll take a look at the equation of the parabola.

Again, given that

`y=a(x-h)^2+k`

And we have:

`y=(x+1)^2-25`

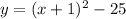
We'll take a look at the 'a' value. Seeing that there is no coefficient this would mean that a = 1.

Since a is