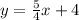To find the line that is perpendicular to the one we have, the first step is to rewrite the expression in the slope-intercept form.
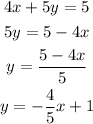
The slope of this line is -4/5. The one that is perpendicular to it has a slope that is negative reciprocal to this one, which means that we need to invert the fraction and the signal.
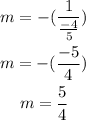
The equation for the perpendicular line so far is:
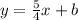
To find "b" we need to replace the coordinates of (-4,-1) and solve for b.
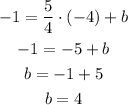
The full expression is: