Answer:
Step-by-step explanation:
Given:

B.)
To find the vertex, we use the following formula:
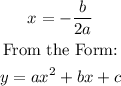
So based on the given equation, the values of a and b are:
a=3
b=12
We plug in what we know:
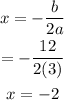
Next, we plug in x=-2 into g(x)=3x^2+12x+9:
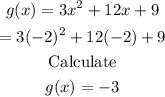
Therefore, the vertex is (-2,-3).
C.
Now, to find the axis of symmetry, we also use the formula x=-b/2a since it is the vertical line that goes through the vertex.
Therefore, the Axis of Symmetry for the given equation is x = -2.
D.
We let g(x)=0 to find the x-intercept:

Based on the factors, the values for x are:
x=-1
x=-3
Therefore, the x intercept points are:
(-1,0),(-3,0)
To get the y-intercept, we let x=0 and plug in into g(x)=3x^2+12x+9. So,
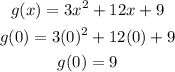
Therefore, the y intercept point is (0,9).