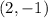Use the elimination method to solve the system of equations:
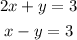
Add both equations to eliminate the variable y. This can be done because the coefficient of y in the first equation is 1, while the coefficient of y in the second equation is -1:

Replace x=2 into the first equation and solve for y:
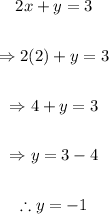
Then, the solution to the system is x=2 and y=-1. Using the ordered pair notation (x,y), the solution to the system is (2,-1).
Therefore, the correct choice is: