Question

Triangle JKL is an equilateral triangle with two of its vertices at points J and K. What are the coordinates of point L? Round to the nearest tenth as needed.

Answer 1

(6, 7.2)

Explanation:

Since it is an equilateral triangle, all of the side lengths must be equal.

Therefore, we know the lengths JK = 6 and JL = 6. If h is the height of the triangle, the Pythagoras's theorem says

`((JK)/(2))^2+h^2=JL^2`

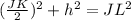
putting in the values of JK and JL gives

`((6)/(2))^2+h^2=6^2`
`3^2+h^2=6^2`

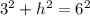
subtracting 3^2 from both sides gives

`h^2=6^2-3^2`
`h^2=27`

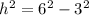
Taking the square root of both sides gives

`h=3\sqrt[]{3}`

or in decimal form rounded to the nearest tenth

`h=5.2`

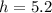
With the value of h in hand, we can now read off the coordinates of L.

The x coordinate of L is 6 (count the boxes along the x-axis until you are under L or halfway between J and K).

The y-coordinate of L is 2 + h = 2 + 5.2 = 7.2 ( how far above the x-axis the traingle is plus the height of the triangle ).

Hence, the coordinates of the point L are (6, 7.2).