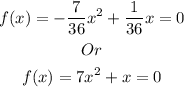Question

Find a quadratic function with the given zeros and passing through the given point.

Answer 1

The Solution.

The given zeros of the quadratic function are

`x=(1)/(7),x=0`

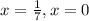
This implies that

`\begin{gathered} x=(1)/(7) \\ \text{cross multiplying, we get} \\ 7x=1 \\ 7x-1=0 \\ \text{ Similarly, x=0} \end{gathered}`

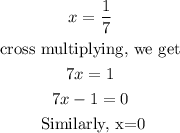
The required quadratic function can be obtained as below:

`\begin{gathered} (7x-1)x=0 \\ \text{Clearing the bracket, we get} \\ f(x)=7x^2-x=0 \end{gathered}`

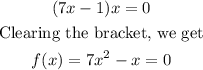
So, the required quadratic function is

`\begin{gathered} f(x)=a(7x^2-x=0)\ldots\text{eqn}(1) \\ \text{where a is a constant, to be determined.} \end{gathered}`

To find the value of a, we shall apply the given initial values, that is,

`(4,-3)\Rightarrow x=4,f(x)=-3`

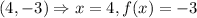
We get,

`-3=a\lbrack7(4^2)-4\rbrack`
`\begin{gathered} -3=a(7*16-4) \\ -3=a(112-4) \end{gathered}`
`\begin{gathered} -3=a(108) \\ -3=108a \\ \text{Dividing both sides by 108, we get} \\ a=-(3)/(108) \\ \\ a=-(1)/(36) \end{gathered}`
`\text{ Substituting -}(1)/(36)\text{ for a in eqn(1) above, we get}`
`\begin{gathered} f(x)=-(1)/(36)(7x^2-x=0) \\ \\ f(x)=-(7)/(36)x^2+(1)/(36)x=0\text{ } \\ Or \\ \text{Multiplying through the equation by 36, we get} \\ 7x^2+x=0 \end{gathered}`

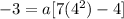
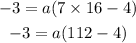
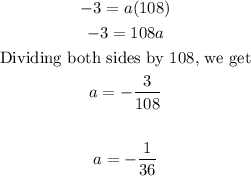
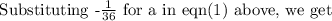
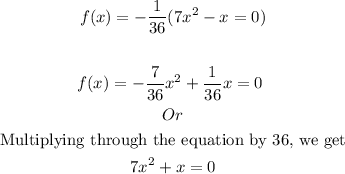
Hence, the correct quadratic function is

`\begin{gathered} f(x)=-(7)/(36)x^2+(1)/(36)x=0 \\ Or \\ f(x)=7x^2+x=0 \end{gathered}`