This is the answer tab
Firstly, we need to write the formulas for both the gravitational force and electric force. Our gravitational force is:
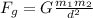
And the electric force is:
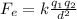
We can see that these forces have almost equal formulas. What we want is Fe/Fg. Before this, we can simplify the forces, as both particles have the same charge and mass. We're left with the following:
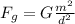
And

By dividing both, we get
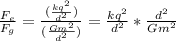
We have d^2 on the numerator and denominator. We can elimante the distance then, as it is different from zero. We have the following:

We can then replace our values with the constants. k is Coulomb's constant, q is the charge of a proton, G is Newton's constant, and m is the mass of a proton. We finally get
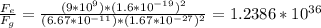
So, the electric force is 1.2386*10^36 times higher than the gravitational. The most interesting about this, is that it doesn't depend on the distance the two of them are apart.