Question

Determine if the sequence converges or diverges 8, 108, 208, 308, 408

Answer 1

Hello there. To solve this question, we'll have to remember some properties about convergence of sequences.

Given the following sequence:

`\mleft\lbrace a_1,a_2,\ldots,a_n\mright\rbrace`

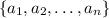
If it is a finite sequence, then it converges to its last term, that is the lim sup (or greatest term of the sequence).

If it is infinite, then the sequence only converges if this limit exists and is equal to zero, that is:

`\lim _(n\rightarrow\infty)a_n=0`

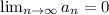
With this, we'll be able to determine whether the following sequence is convergent or not:

`S=\mleft\lbrace8,108,208,308,408\mright\rbrace`

Since it is a finite sequence, we already know it converges.

The lim sup of this sequence is its largest term, in this case, 408, and we write:

`\limsup S=408`

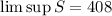
If it was an infinite sequence, on the other hand, we would have to determine the general term a_n and see if the limit is equal to zero.

Notice that there is a pattern between the values: the difference between two consecutive numbers is equal to 100.

In other words, it is an arithmetic progression with ratio equal to 100.

This means that we can use the following formula:

`a_n=a_1+(n-1)\cdot r`

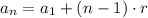
Where a_1 = 8 and r = 100, therefore:

`\begin{gathered} a_n=8+(n-1)\cdot100 \\ a_n=8+100n-100 \\ a_n=100n-92 \end{gathered}`

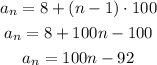
And taking the limit as it goes to infinity, we have that:

`\lim _(n\to\infty)a_n=\lim _(n\to\infty)100n-92=\infty`

That is, the limit is not zero (not even a real number), so the sequence would not converge.