Question

The MACH 5 car goes around a curve with a speed of 20.0 m/s experiencing a centripetalacceleration of 3.80 m/s2. What is the radius of the curve in meters? Round your answer correctly tothe first three places. No need for units for this problem.

Answer 1

Given data:

Velcoity of the car along the curve;

`v=20.0\text{ m/s}`

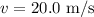
Centripetal acceleration of the car;

`a_c=3.80\text{ m/s}^2`

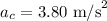
The centripetal acceleration is given as,

`a_c=(v^2)/(r)`

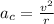
Here, r is the radius of the curve.

Rearranging the above equation to get an expression for radius of curve,

`r=(v^2)/(a_c)`

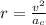
Substituting all known values,

`\begin{gathered} r=((20)^2)/(3.80) \\ =105.26\text{ m} \\ \cong105\text{ m} \end{gathered}`

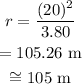
Therefore, the radius of the curve is 105 m.