Given data:
* The total mass of an astronaut and equipment is,
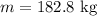
* The force is given as,
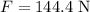
* The time taken is,
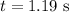
Solution:
According to the Newton's second law,
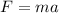
where a is the acceleration of the body,
Substituting the known values,
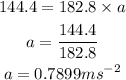
By the kinematic equations,
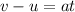
where u is the initial velocity and v is the final velocity,
Substituting the known values,

The average speed of the astronaut is,
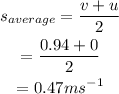
The average speed of the astronaut in Km/h is,
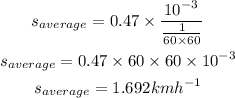
Thus, the average speed of the astronaut is 1.692 km/h.