Question

Jim has a new job and earns a salary of $46,000. Valorie has a new job and earns a salary of $59,000. Jim will receive a salary increaseof $2,700 per year and Valorie will receive a salary increase of $1,500 per year. Based on this information, which TWO statements arecorrect?es )A)It will take 10 years for Jim to earn the same salary as Valorie.B)It will take 12 years for Jim to earn the same salary as Valorie.D)When solved for x, 46,000x + 2,700 = 58,000x + 1,500 gives the number ofyears it will take Jim to earn the same salary as Valorie.When solved for x, 46,000 + 2,700x = 58,000 + 1,500x gives the number ofyears it will take Jim to earn the same salary as Valorie.When solved for x, 46,000x + 2,700x = 58,000x + 1,500x gives the numberof years it will take Jim to earn the same salary as Valorie.E)

Answer 1

Let's use the variable x to represent the number of years.

So, if the initial salary of Jim is $46,000 and it increases by $2,700 each year, after x years, his salary is:

`46000+2700x`

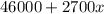
Doing the same for Valorire, her salary is:

`58000+1500x`

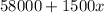
In order to find after how many years their salary will be the same, we can equate both salaries and calculate the value of x:

`\begin{gathered} 46000+2700x=58000+1500x \\ 2700x-1500x=58000-46000 \\ 1200x=12000 \\ x=(12000)/(1200) \\ x=10 \end{gathered}`

So let's check each option:

A.

True, it takes 10 years to they have the same salary.

B.

False, after 12 years Jim's salary is higher than Valorie's salary.

C.

False, the variable x should multiply the increase per year in the salary, not the initial salary.

D.

True, that's the equation and procedure we used.

E.

False, the variable x should multiply just the increase per year in the salary, not the initial salary.

So the correct options are A and D.