Question

When the function f(x) is divided by x-3, the quotient is 2x^2 – 5x-5 and theremainder is 9. Find the function f(x) and write the result in standard form.

Answer 1

We need to find a polynomial in standard form. For this, we have:

Divisor (d):

`Divisor(d)\Rightarrow x-3`

Quotient (q):

`\text{Quotient(q)}=2x^2-5x-5`

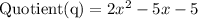
Remainder (R):

`R=9`

Then, we know that if we have all of these "components", we can use them using the following formula:

`D=d\cdot q+R`

This is the formula to find the dividend of a division. Then, we have that the function f(x) will be:

`D=(x-3)(2x^2-5x-5)+9_{}`

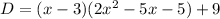
To solve this, we need to multiply the binomial (x - 3) by the trinomial as follows:

1. The unknown variable x by any of the terms of the trinomial:

`x(2x^2)+x(-5x)+x(-5)=2x^3-5x^2-5x`

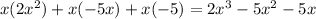
2. And we need the latter to the result of multiplying -3 by any of the terms of the trinomial:

`-3(2x^2)-3(-5x)-3(-5)=-6x^2+15x+15`

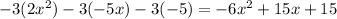
Now, we need to add both partial results as follows (we need to add like terms):

`2x^3-5x^2-5x-6x^2+15x+15`
`2x^3-5x^2-6x^2-5x+15x+15`
`2x^3-11x^2+10x+15`

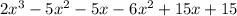
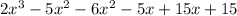
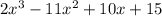
And now, we need to add the remainder:

`D=2x^3-11x^2+10x+15+9\Rightarrow D=2x^3-11x^2+10x+24`

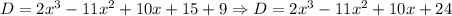
Therefore, the function is:

the dividend of a division. Then, we have