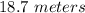Question

A person stands 5 meters from a building. The angle of elevation to the top of the building is 75°. Find the height of the building to the nearest tenth.

Answer 1

Using the information given in the exercise, you need to draw the following Right triangle (It is not drawn to scale):

Where "h" is the height of the building in meters.

To find the height, you can use the following Trigonometry Identify:

`\tan \alpha=(opposite)/(adjacent)`

In this case:

`\begin{gathered} \alpha=75\degree \\ opposite=h \\ adjacent=5 \end{gathered}`

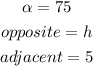
Then, you can substitute values and solve for "h". This is (rounded to the nearest tenth):

`\begin{gathered} \tan (75\degree)=(h)/(5) \\ \\ 5\cdot\tan (75\degree)=h \\ h=18.66 \\ h\approx18.7 \end{gathered}`

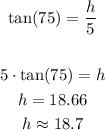
The answer is:

`18.7\text{ }meters`