A table is given. It is required to use the linear regression capabilities to find a linear model for (t, ln(R)) with an equation of the form ln(R)=at+b, and then write in exponential form.
It is also required to use a graphing utility to draw a graph.
(a) Rewrite the table values for t and ln(R) as follows:
Input the values into a graphing utility to find the linear model:
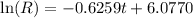
Take the exponent of both sides of the equation to write in exponential form as required:
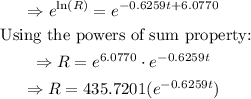
(b) Use the graphing utility to graph the exponential function:
Notice that the graph at the top-right best fits the graph.
(c) Evaluate the definite integral using the graphing utility:
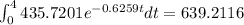
The answer is 639.2116 L.