Question

The temperature is 60F if the temperature will decrease by 3F each hour let H be the number of hours when will the temperature be below 32F

Answer 1

The temperature of the given environment starts at 60ºF and decreases at a constant rate of 3ºF/h. We can write a linear equation for the room temperature as

`T=-3H+60`

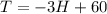
Where H is the number of hours that passed. We want to know when the temperature will be below 32ºF, in another words

`T<32`

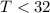
If we substitute the expression for the temperature on the inequality, we're going to have

`-3H+60<32`

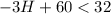
Solving for H:

`\begin{gathered} -3H+60<32 \\ -3H<32-60 \\ -3H<-28 \\ 3H>28 \\ H>(28)/(3) \end{gathered}`