Question

Analytically determine what type(s) of symmetry, if any, the graph of the equation would possess. Show your work.23) 2x^2 -3 = 4|y|

Answer 1

The graph is symmetric about the x-axis, the y-axis, and the origin

Step-by-step explanation:

A graph can be symmetric about the x-axis, about the y-axis, and about the origin.

To know if the graph is symmetric about the x-axis, we need to replace y by -y and determine if the equation is equivalent. So,

If we replace y with -y, we get:

`\begin{gathered} 2x^2-3=4|-y| \\ 2x^2-3=4|y| \end{gathered}`

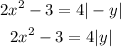
Therefore, the graph is symmetric about the x-axis.

The graph is symmetric about the y-axis if we replace x by -x and we get an equivalent equation. So:

`\begin{gathered} 2(-x)^2-3=4|y| \\ 2x^2-3=4|y| \end{gathered}`

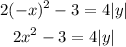
Since both equations are equivalent, the graph of the equation is symmetric about the y-axis

The graph is symmetric about the origin if we replace x by -x and y by -y and we get an equivalent equation. So:

`\begin{gathered} 2(-x)^2-3=4|-y| \\ 2x^2-3=4|y| \end{gathered}`

Therefore, the graph is symmetric about the origin.