Question

A single card is drawn from a standard deck of 52 cards. What is the probability the card is a five OR a six?

Answer 1

Recall that to determine this type of probability we have to determine the number of favorable cases and divide it by the total number of cases.

In this problem, the total number of cases is 52.

Now, recall that in a standard deck there are 4 fives and 4 sixes, then, the number of favorable cases is 4+4=8.

Therefore, the probability that the card is a six or a five is:

`(4+4)/(52)\text{.}`

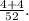
Simplifying the above fraction we get:

`(4+4)/(52)=(8)/(52)=(2)/(13)`

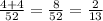
Answer:

`(2)/(13)\text{.}`