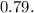Question

A point is chosen at random in the square shown below. Find the probability that the point is in the shaded circular region. Each side of the square is 8 in, andthe radius of the circle is 4 in.Use the value 3.14 for it. Round your answer to the nearest hundredth.

Answer 1

Recall that, to solve this kind of problem, we can use the folllowing expression to determine the probability:

`\frac{\text{favorable cases}}{total\text{ cases}}.`

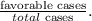
Now, we have to identify which are the favorable cases, in the given problem, we want the probability that the point is in the shaded region, therefore, the favorable cases would be represented by the area of the shaded region. The total cases are represented by the area of the whole region.

Using the formula for the area of a circle, we get that:

`A_c=\pi(4in)^2=16\pi in^2.`

Using the formula for the area of a square, we get:

`A_s=(8in)^2=64in^2.`

Finally, using the above expression, we get that the probability of the point being in the shaded region is:

`(A_c)/(A_s)=(16\pi in^2)/(64in^2)\approx0.79.`

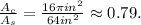
Answer:

`0.79.`