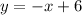Question

Write an equation in slope-intercept form of a line passing through the given point andparallel to the given line.13. (4, 2); x+ y= 1

Answer 1

The equation of the line in slope-intercept form is,

`y=mx_{}+b`

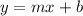
where,

m = slope

The equation of the line given is,

`x+y=1`

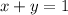
Let us now rearrange the equation in the slope-intercept form in order to obtain the slope.

Therefore,

`\begin{gathered} x+y=1 \\ y=-x+1 \\ \therefore\text{ The slope(m) is -1.} \end{gathered}`

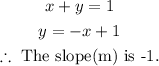
We were told the point is parallel to the equation of the line.

The rule for parallelism is,

`\begin{gathered} m_1=m_2 \\ \therefore-1=-1 \end{gathered}`

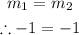
The formula to calculate for the equation of a line given one point is,

`y-y_1=m(x-x_1)`

Given

`\begin{gathered} (x_1,y_1)=(4,2) \\ m=-1 \end{gathered}`

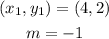
Substitute and simplify

`\begin{gathered} y-2=-1(x-4) \\ y-2=-1x+4 \\ y=-x+4+2 \\ \therefore y=-x+6 \end{gathered}`

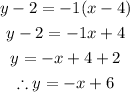
Hence, the equation of the line in slope-intercept form is

`y=-x+6`