Question

evaluate the function over the domain {-1, 0, 1, 2}. as the values of the domain increase, do the values of the function increase or decrease? y=2*3^-1

Answer 1

To evaluate a function with a specific value in the domain you susbtitute in the equation of the function the independient variable (x) for the value in domain.

`y=2\cdot3^x`

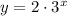
For x = -1 (a number n powered to a negative number (m) n^-m is equal to 1/n^m

`y=2\cdot3^(-1)=2\cdot(1)/(3)=(2)/(3)\approx0.66`

For x=0 (any number powered to 0 is equal to 1)

`y=2\cdot3^0=2\cdot1=2`

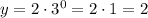
For x = 1

`y=2\cdot3^1=2\cdot3=6`

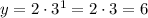
For x = 2

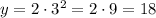
`y=2\cdot3^2=2\cdot9=18`Then, as you can see as the values of the domain increase, the values of the function increase