We are given that a car skids 34 meters before stopping with an acceleration of 8.2 meters per second squared. To determine the initial velocity we will use the following equation of motion:

Since the car stops completely the final velocity is zero, therefore, we have:
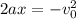
Now we replace the following values:
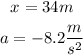
The acceleration has a negative sign because the car is decelerating. Replacing the values:
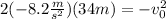
Now we solve the operations on the left side of the equation:
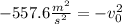
Now we multiply both sides by -1:

Now we take the square root to both sides:
![\sqrt[]{557.6(m^2)/(s^2)}=√(v^2_0)](https://img.qammunity.org/2023/formulas/physics/college/nx76h8dkaen7c8bb2thi5dkinie0kalz16.png)
Solving the operations:
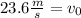
Therefore, the initial velocity is 23.6 meters per second.