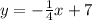Question

Write an equation of a line parallel to the given equation through the given point

Answer 1

Given the equation of the line :

`y=-(1)/(4)x-6`

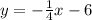
It is required to write the equation of the line parallel to the given line and pass through the point ( 12 , 4 )

The general equation of the line in slope - intercept form is :

`y=m\cdot x+b`

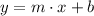
Where m is the slope and b is y - intercept

As the line are parallel , so, the slope of the required line will be equal to the slope of the given line

So, the slope = m = -1/4

So, the equation of the line will be :

`y=-(1)/(4)x+b`

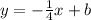
Using the given point ( 12 , 4 ) to find b

so, when x = 12 , y = 4

`\begin{gathered} 4=-(1)/(4)\cdot12+b \\ \\ 4=-3+b \\ 4+3=b \\ b=7 \end{gathered}`

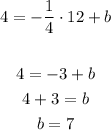
So, the equation of the required line is :

`y=-(1)/(4)x+7`