Given:
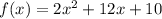
a) Standard form of the function is,
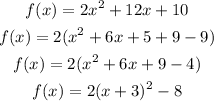
Standard form is,
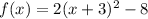
b) The vertex of the given function
The vertex of the parabola having form,
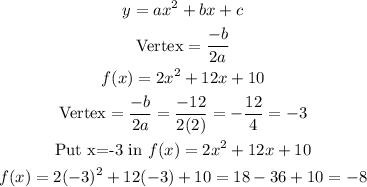
Vertex is ( -3,-8)
c) x and y-intercept is,
![\begin{gathered} Set\text{ y=0 that means f(x)=0} \\ f(x)=2x^2+12x+10 \\ 2x^2+12x+10=0 \\ 2(x^2+6x+5)=0 \\ x^2+6x+5=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a},a=1,b=6,c=5 \\ x=(-12\pm√(12^2-4\cdot\:2\cdot\:10))/(2\cdot\:2) \\ x=(-12\pm\: 8)/(4) \\ x=-1,x=-5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/sgirkmnnv29rzd7rhhiseh7a48efl6jmib.png)
x- intercepts are (-1,0) and (-5,0).
For y-intercept , set x=0
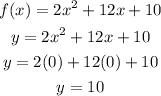
y-intercept is (0,10)
d) the graph of the function is,
e) The domain and range of the function is,
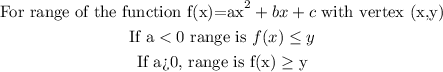
For the given function,
![\begin{gathered} f(x)=2x^2+12x+10\text{ with vertex (-3,-8)} \\ a=2>0,\text{ range is f(x)}\ge\text{-8} \\ \text{Domain is -}\inftyTherefore,[tex]\begin{gathered} \text{Domain of f is (-}\infty,\infty) \\ \text{Range of f is \lbrack-8,}\infty) \end{gathered}]()