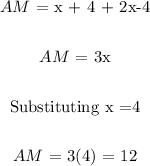The measure of AM is 12
Here, we are to find the measure of AM
Mathematically, the centroid divides the median on which it lies into 2 parts
These parts are usually in the ratio 1 to 2
What this mean is that if we multiply the smaller side by 2, we get the larger side
That would proceed as follows;
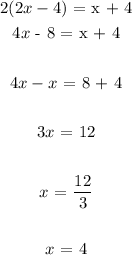
Now, the length of the median is the sum of the two parts
Mathematically, that would be;