Question

Solve the following using the elimination method 3s + 9c = 758s + 5c = 67

Answer 1

Given:

`\begin{gathered} 3s+9c=75 \\ 8s+5c=67 \end{gathered}`

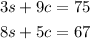
To use the elimination method, one of the variables must have the same coefficient before eliminating.

Hence, to eliminate the variable c, make the coefficient the same by multiplying equation (1) by 5 and equation (2) by 9.

`\begin{gathered} 3s+9c=75.............(1)*5 \\ 8s+5c=67............(2)*9 \\ \\ The\text{ new equations are:} \\ 15s+45c=375................(1) \\ 72s+45c=603...............(2) \end{gathered}`

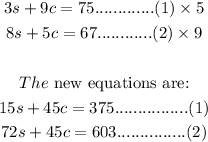
Subtract the new equation (1) from equation (2):

`\begin{gathered} equation\text{ \lparen2\rparen-equation \lparen1\rparen;} \\ 57s=228 \\ s=(228)/(57) \\ s=4 \end{gathered}`

Substitute s = 4 into equation (1);

`\begin{gathered} 3s+9c=75 \\ 3(4)+9c=75 \\ 12+9c=75 \\ 9c=75-12 \\ 9c=63 \\ c=(63)/(9) \\ c=7 \end{gathered}`

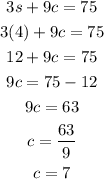
Therefore;

s = 4

c = 7