Question

Can someone pls help me with this I'm soconfused thank u

Answer 1

The population of cockroaches grows exponentially. 2 months ago there were 3 cockroaches, now there are 18.

As this is exponential growth, it can be modeled with the following formula:

`y(t)=a.(e^k)^t`

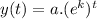
Applying the laws of exponents, this is equivalent to:

`y(t)=a.e^k^t`

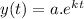
where y(t) is the number of cockroaches at time t, a is the initial population. In this case, we want to find k.

Now, we know a=3, t=2, and right now y(2)=18:

`18=3.e^(2k)`

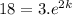
this is equivalent to:

`6=e^(2k)`

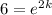
Take the natural logarithm of both sides:

`\ln (6)=\ln (e^(2k))`

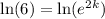
this is equivalent to:

`\ln (6)=2k`

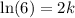
solving for k, we get:

`k\text{ =}(\ln (6))/(2)`

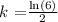
Therefore, we have created a real-life problem that uses the laws of exponents.