Question

Solve.(z-2)(z-1)=0(If there is more than one solution, separate them with commas.)= 0Z=80,0,...Ś

Answer 1

We have the equation:

`(z-2)(z-1)=0`

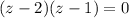
There are a total of two options that complies the equation, as it is a product.

If the first term is 0, the equation is right.

But if the second term is 0, the equation is right too.

Then both are solutions.

So we have:

`z-2=0`
`z=2`

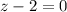
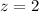
And,

`z-1=0`
`z=1`

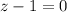
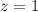
Then we can conclude:

The two correct answers are z=2 and z=1

z=1,2 in the format asked.