Question

THE CORNER POINTS OF THE SHADED REGION IN A LINEAR PROGRAMING PROBLEM ARE (7,0) (9,-1) (9,5) (8,6) AND (0,6) IF THE COST FUNCTION WAS GIVEN BY C=3X+Y WHAT WILL THE MINIMUM COST BE?

Answer 1

Given:

The shaded region are (7,0) (9,-1) (9,5) (8,6), and (0,6).

The cost function is

`C=3x+y`

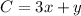
Required:

We need to find the minimum cost.

Step-by-step explanation:

Consider the point (7,0).

Substitute x =7 and y=0 in the given function.

`C=3(7)+0=21`

Consider the point (9,-1).

Substitute x =9 and y=-1 in the given function.

`C=3(9)+(-1)=27-1=26`

Consider the point (9,5).

Substitute x =9 and y=5 in the given function.

`C=3(9)+5=27+5=32`

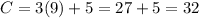
Consider the point (8,6).

Substitute x =8 and y=6 in the given function.

`C=3(8)+6=24+6=30`

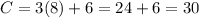
Consider the point (0.6).

Substitute x =0 and y=6 in the given function.

`C=3(0)+6=6`

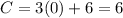
We know that the lowest value of 21, 26, 32, 30, and 6 is 6.

The minimum cost will be 6.

Final answer:

The minimum cost will be 6.