Question

Is (0,0) a solution to this system?y? x2 + x - 4y> x2 + 2+ 2x + 1A. No. (0,0) does not satisfy either inequality.B. No. (0,0) satisfies y? x2 + x - 4 but does not satisfy y> x2 + 2x+1.C. No. (0,0) satisfies y> x2 + 2x+1 but does not satisfy y>yz x2 + x-4.D. Yes. (0,0) satisfies both inequalities.

Answer 1

Option B: (0, 0) satisifes y >= x^2 + x - 4 while it does not satisfy y > x^2 + 2x + 1

Step-by-step explanation

We are given two inequalities:

`\begin{gathered} y\text{ }\ge x^2\text{ + x - 4} \\ y>x^2\text{ + }2x\text{ + 1} \end{gathered}`

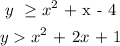
To check if (0, 0) satisifes both inequalities, we have to put the values of x and y as 0 and see if the resulting inequality is mathematically correct.

We have that:

`\begin{gathered} 0\text{ }\ge0^2\text{ + 0 - 4} \\ \Rightarrow\text{ 0 }\ge\text{ -4} \\ \text{and} \\ 0>0^2\text{ + 2(0) + 1} \\ 0\text{ > 1} \end{gathered}`

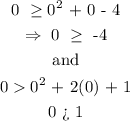
As we can see, (0, 0) satisifes the first inequality while it does not satisfy the second one.

The answer is Option B