Question

A kite is on a string as shown in the figure below. 120 feet 60° The string makes an angle of 60° with the ground. If the length of the string is 120 feet, what is the height of the kite above the ground, in feet? (G.8b)(1 point) A. 60 B. 120 O C. 603 D. 1203

Answer 1

The height of the kite above the ground is 60√3. ( option C)

Trigonometric ratio is the ratio of the sides of a right angled triangle.

Some of the trigonometric functions include

sinX = opp/hyp

cosx = adj/hyp

tanx = opp/adj

where x is the acute angle.

The height of the kite to the ground is the opp to angle 60

Therefore;

sin60 = opp/120

let opp = y

sin60 = √3/2

√3/2 = y/120

120√3 = 2y

y = 60√3

Therefore the height of the kite from the ground is 60√3

Answer 2

We are given the length and angle of a string attached to a kite and we are asked about the height of the kite. To find the height we need to have into account that the string and the height form a right triangle, with the height being the opposite side of the 60 degrees angle, and the string being the hypotenuse, therefore, we can use the sine function, since this function is defined as:

`\sin \theta=(opposite)/(hypotenuse)`

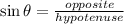
where:

`\begin{gathered} \text{opposite}=\text{height}=h \\ \text{hypotenuse}=120 \\ \theta=60^0 \end{gathered}`

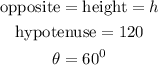
Replacing these values we get:

`\sin 60=(h)/(120)`

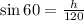
Solving for "h"

`h=120\sin 60`

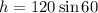
Solving the operation we get:

`h=60\sqrt[]{3}`

These result from the fact that:

`\sin 60=\frac{\sqrt[]{3}}{2}`