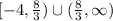Question

Find the domain of the function.✓4+xf(x) =8-3xWrite your answer as an interval or union of intervals.

Answer 1

The domain is the set of possible x-values. In our case, f(x) is definined when the term into the radical is greater or equal than zero and the denominator is different from zero, that is,

`\begin{gathered} 4+x\ge0 \\ \text{and} \\ 8-3x\\e0 \end{gathered}`

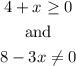
From the inequality, we get

`x\ge-4`

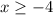
and, from the last relation, we have

`\begin{gathered} -3x\\e-8 \\ so \\ x\\e(8)/(3) \end{gathered}`

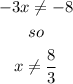
By combining both results, the domain is

`\lbrack-4,(8)/(3))\cup((8)/(3),\infty)`