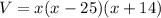The volume of a prism is given by:
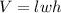
We know that the height is x. The length is 25 shorter than x, this can be express as:

The width is 14 longer than x, this can be express as:
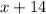
Plugging the expressions for the length, the width and the height we have that:
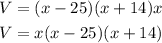
Therefore, the volume of the prism is: