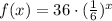Question

Define an exponential function, f(x), which passes through the points (0,36) and(2,1). Enter your answer in the form a · b^xf(x) =

Answer 1

The general form of the exponential function is:

`f(x)=a\cdot b^x`

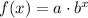
we will find the equation of the exponential function which passes through the points (0, 36) and (2, 1)

So,

when x = 0, f(0) = 36

`\begin{gathered} 36=a\cdot b^0 \\ 36=a\cdot1 \\ a=36 \end{gathered}`

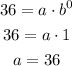
and when x = 2, f(x) = 1

Using the substitution with a = 36

So,

`\begin{gathered} 1=36\cdot b^2 \\ b^2=(1)/(36) \\ \\ b=\sqrt[]{(1)/(36)}=(1)/(6) \end{gathered}`

So, the answer will be the equation of the function is:

`f(x)=36\cdot((1)/(6))^x`