Given:
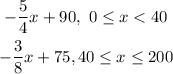
Required:
Which table would be used to graph a piece of the function.
Step-by-step explanation:
Here the function is broken at the three points x=0, x=40, x=200.
So we will choose that table in which the values of x are 0,40,200.
In this table, you can see the values of x are 0,40, and 200.
Final Answer:
The correct answer is