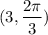The point that shows the correct location for the polar coordinate
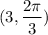 is **point D**.
is **point D**.
Here's how to find it:
1. **Remember the relationship between polar and rectangular coordinates:** In a polar coordinate system, a point is represented by its distance from the origin (r) and the angle it makes with the positive x-axis (θ). We can convert between polar and rectangular coordinates using the following formulas:
x = r cos(θ)
y = r sin(θ)
2. **Plug in the given values:** In this case, r = 3 and θ =
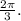 Therefore:
Therefore:
x = 3 cos
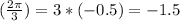
y = 3 sin
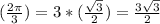
3. **Plot the point:** Based on the calculations, the point should be plotted at
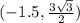 . Looking at the provided image, this corresponds to **point D**.
. Looking at the provided image, this corresponds to **point D**.
Therefore, **point D** is the correct location for the polar coordinate