ANSWER
Step-by-step explanation
Given that;
The speed of the pilot = 670 miles per hour
The first path took her 1 hour 30 minutes
The second path took her 2 hours
Included angle = 170 degrees
To find the distance from the starting position, follow the steps below
Step 1; Find the distance of the first and second path
Recall, that
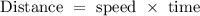
For the first leg
time = 1 hour 30 minutes
speed = 670 miles per hour
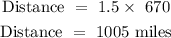
The first leg = 1005 miles
Second leg
time = 2 hours
speed = 670 miles per hour
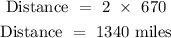
The second leg = 1340 miles
apply the cosine rule to find the distance from the starting position
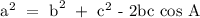
substitute the given data into the cosine formula

Therefore, distance from the starting position is 2336.3 miles