Question

All you need is in the photo please answer fast pleaseee pleaseeeeeeeeeeee4p+2g=963p+1g=60

Answer 1

The given equations are in standard form, first, write them in slope-intercept form.

"p" is the variable in the x-axis

"g" is the variable in the y-axis

First equation

`\begin{gathered} 4p+2g=96 \\ 2g=96-4p \\ (2g)/(2)=(96)/(2)-(4p)/(2) \\ g=-2p+48 \end{gathered}`

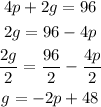
Second equation

`\begin{gathered} 3p+1g=60 \\ g=60-3p \end{gathered}`

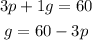
Next, you have to determine two points for each equation, the easiest point to determine is the y-intercept, just replace the formula with p=0

For the second point, you can choose any value of p, for example, p=10

First equation

For p=0

`\begin{gathered} g=-2p+48 \\ g=-2\cdot0+48 \\ g=48 \end{gathered}`

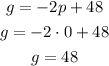
The first point is (0,48)

For p=10

`\begin{gathered} g=-2\cdot10+48 \\ g=-20+48 \\ g=28 \end{gathered}`

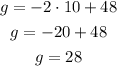
The second point is (10,28)

Plot the points and link them with a line.

Second equation

For p=0

`\begin{gathered} g=-3p+60 \\ g=-3\cdot0+60 \\ g=60 \end{gathered}`

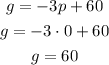
The first point is (0,60)

For p=10

`\begin{gathered} g=-3\cdot10+60 \\ g=30 \end{gathered}`

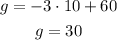
The second point is (10,30)

Plot both points and link them to determine the line