Question

Can someone walk me through this? I know it’s familiar but I can’t recall how to do it.

Answer 1

18 dimes and 6 quarters

1) Let's recall that 1 dime = $0.10 and a quarter is $0.25

2) We can solve this by writing a Linear System of Equations:

`\begin{gathered} x+y=24 \\ 0.1x+0.25y=3.3 \end{gathered}`

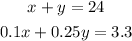
Note that the second equation relates the quantities in dollars, 330 cents is the same as $3.30.

2.2) So now let's solve it using the Elimination Method multiplying one of those equations by -0.1:

`\begin{gathered} 0.1x+0.25y=3.3 \\ -0.1x-0.1y=-2.4 \\ ---------------- \\ 0.15y=0.9 \end{gathered}`

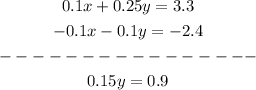
Let's divide both sides by 0.15:

`\begin{gathered} (0.15y)/(0.15)=(0.9)/(0.15) \\ y=6 \end{gathered}`

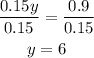
So we have 6 coins of quarters, now let's plug into the original equation x+y=24 to get the number of dimes:

`\begin{gathered} x+6=24 \\ x+6-6=24-6 \\ x=18 \end{gathered}`

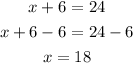
3) Hence, there are 18 dimes and 6 quarters