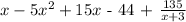Let's first get the coefficients of the numerator: x^4 - 2x^3 + x + 3 = 1, -2, 0, 1, 3
There is no x^2 in the expression, thus, the coefficient for x^2 = 0
Zero of the denominator: x + 3; x = -3
Using synthetic division,
-3 I 1 -2 0 1 3
I_________________
-3 I 1 -2 0 1 3
I_________________
1
-3 I 1 -2 0 1 3
I_____-3___________
1 -5
-3 I 1 -2 0 1 3
I_____-3__15_______
1 -5 15
-3 I 1 -2 0 1 3
I_____-3__15_-45____
1 -5 15 -44
-3 I 1 -2 0 1 3
I_____-3__15_-45____
1 -5 15 -44
-3 I 1 -2 0 1 3
I_____-3__15_-45_132__
1 -5 15 -44 135
The remainder is 135. Which transforms it into 135/x+3.
Thus, the quotient of x^4 - 2x^3 + x + 3 divided by x + 3 is: