Question

KLM~PQR with a scale factor of 3:5, find the perimeter of PQR

Answer 1

We have:

KL = 6

KM = 12

LM = 15

And the given scale factor is 3:5.

The KLM and PQR triangles are similar, therefore:

KL:PQ = 3:5

KM:PR = 3:5

LM:QR = 3:5

This can also be expressed as a fraction:

`(KL)/(PQ)=(3)/(5)`

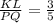
Substitue KL = 6 and find PQ:

`\begin{gathered} (6)/(PQ)=(3)/(5) \\ 6\cdot5=3\cdot PQ \\ 30=3\cdot PQ \\ (30)/(3)=(3PQ)/(3) \\ PQ=10 \end{gathered}`

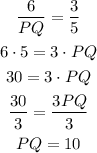
For side PR:

`(KM)/(PR)=(3)/(5)`

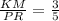
KM = 12, so:

`\begin{gathered} (12)/(PR)=(3)/(5) \\ 12\cdot5=3\cdot PR \\ 60=3\cdot PR \\ (60)/(3)=(3PR)/(3) \\ PR=20 \end{gathered}`

And for side QR:

`(LM)/(QR)=(3)/(5)`

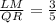
LM = 15, then:

`\begin{gathered} (15)/(QR)=(3)/(5) \\ 15\cdot5=3\cdot QR \\ 75=3\cdot QR \\ (75)/(3)=(3QR)/(3) \\ QR=25 \end{gathered}`

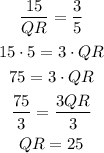
Next, the perimeter is given by:

`P=PQ+PR+QR=10+20+25=55`

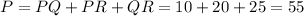
Answer: The perimeter of ΔPQR is 55.